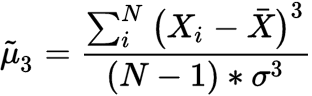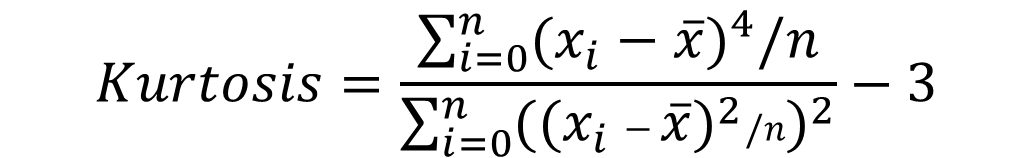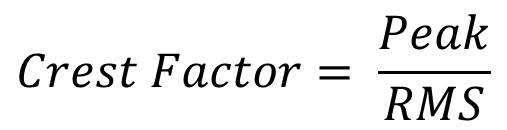안녕하세요, AI 기반 예지보전 솔루션 모터센스입니다.
지난번에는 Spectral Leakage와 Window Function에 대해 알아봤습니다.
만약 해당 게시글을 보지 않았다면, 아래의 링크를 참고해 주세요.
오늘은 진동 크기를 제외하고 진동을 분석할 수 있는 다른 지표들에 대해 알아보고자 합니다.
진동의 크기에 대해서 언급했었습니다.
다시 한번 되짚어 보자면
진동 Waveform의 크기를 표현하는 방법은 RMS, Peak, Peak-to-Peak 등을 사용합니다.
하지만 회전 기계의 예지 보전은 이러한 진동 크기 변화만을 가지고 하지는 않습니다.
진동 Waveform의 크기 이외에 진동 분석에 사용할 수 있는 지표들은 무엇이 있으며,
이 지표들이 어떠한 의미가 있는지 알아봅시다.
참고 Skewness, 왜도
0. 기본 개념
Skewness, 왜도란?
Sampling 된 Waveform 데이터의 분포가 한쪽으로 치우친 정도를 나타내는 척도입니다.
(출처: 마경근의 brunch)
데이터를 위와 같이 확률 밀도 분포를 그렸을 때,
•
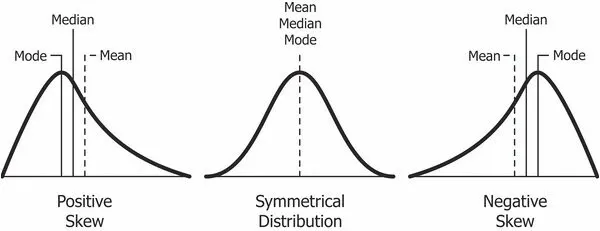
왼쪽 이미지와 같이 오른쪽(양수 방향)으로 꼬리가 길면, 최빈값(Mode) < 중앙값(Median) < 평균(Mean)의 형태가 되어 왜도의 값은 양수(Positive)가 됩니다.
•
오른쪽 이미지와 같이 왼쪽(음수 방향)으로 꼬리가 길면, 평균(Mean) < 중앙값(Median) < 최빈값(Mode)의 형태가 되어 왜도의 값은 음수(Negative)가 됩니다.
•
마지막으로, 가운데처럼 치우침이 없는 경우, 평균(Mean) = 중앙값(Median) = 최 빈값(Mode)이므로 왜도의 값은 0(Zero)가 됩니다.
이러한 비대칭의 정도가 커질수록 왜도의 절댓값은 커집니다.
진동 분석에서의 Skewness 사용 용도
진동 Waveform 분포의 비대칭성을 확인할 수 있으며,
Waveform 균형의 판단 및 균형의 변화를 확인할 때 사용할 수 있는 지표입니다.실제 분석에 적용을 해보면 다음과 같습니다.
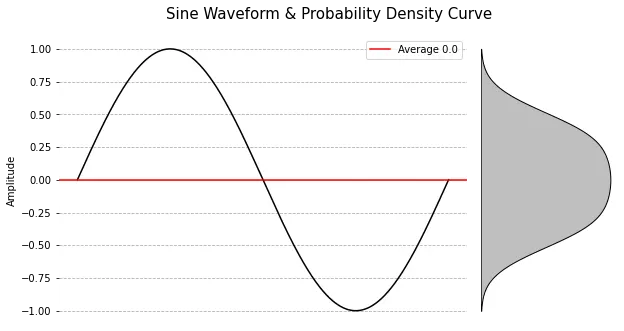
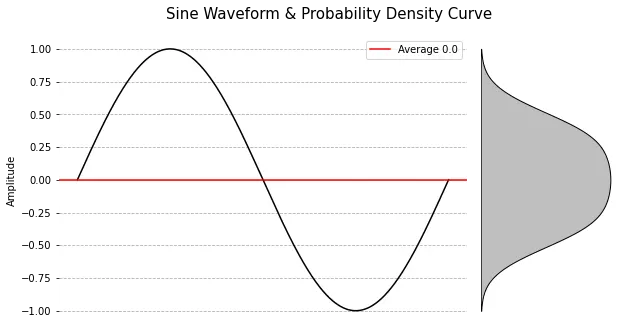
1. Sine Waveform
Sine Waveform의 평균(Average) 0을 기준으로 양의 진폭과 음의 진폭을 반복하는 것이기 때문에
거의 균일한 분포(균등분포, Uniform)를 가지고 있습니다.
균등분포의 경우, 분포 상 치우침이 없기 때문에 Skewness, 왜도는 0(Zero)입니다.
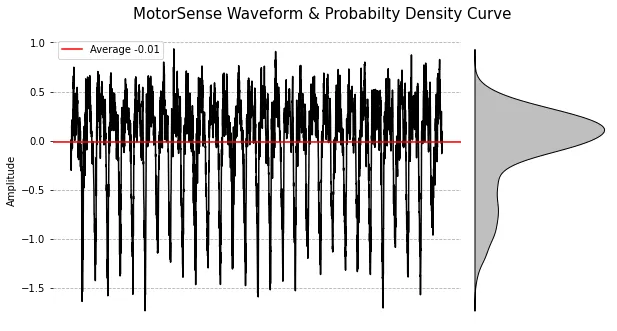
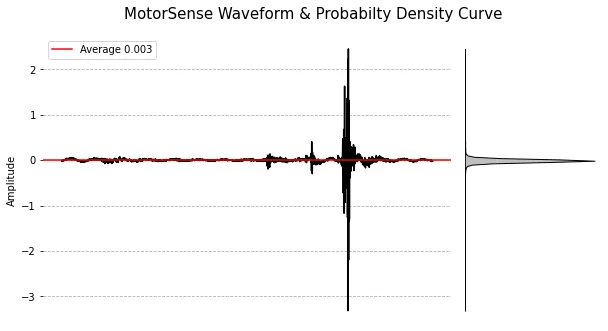
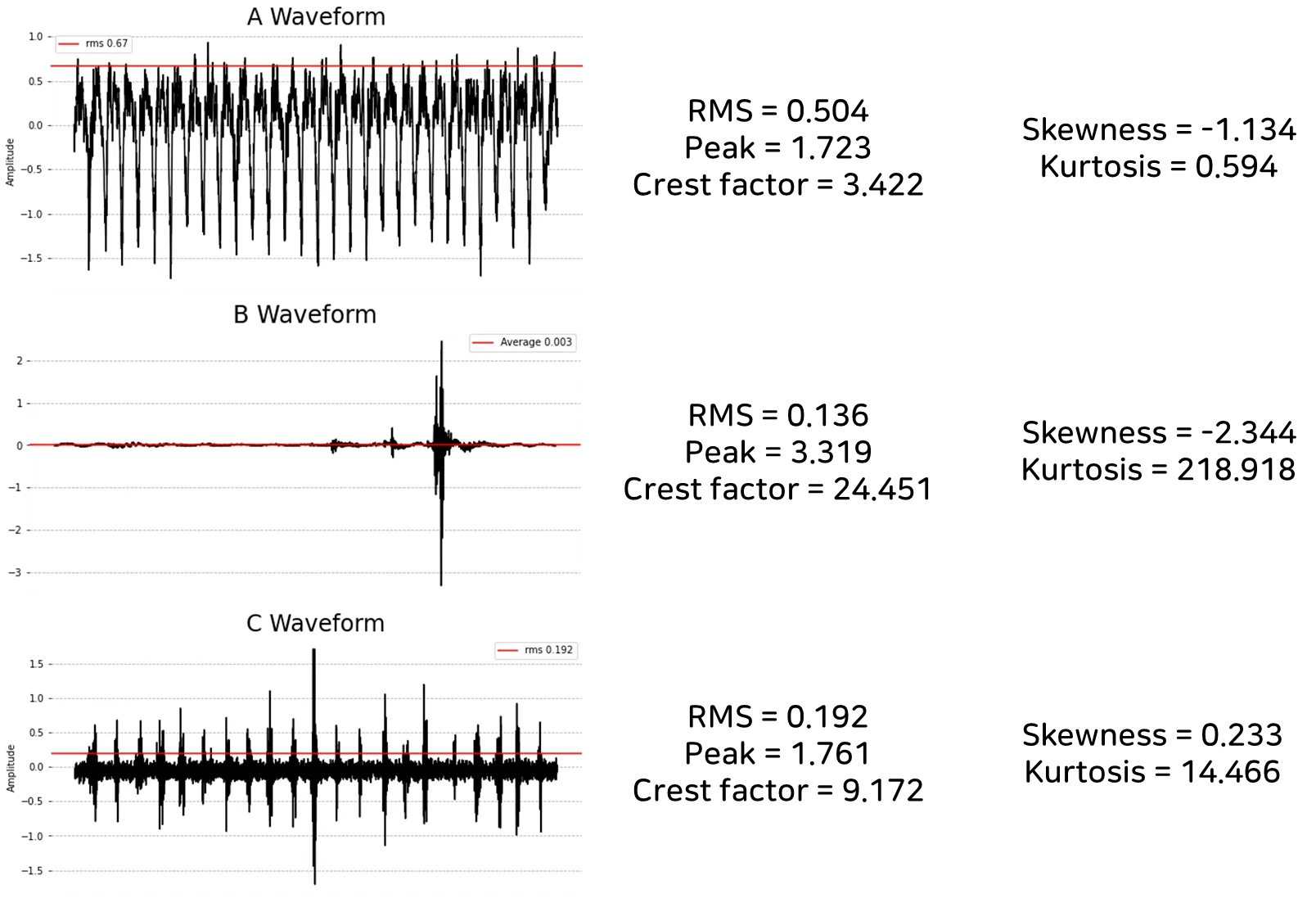
2. MotorSense Example Waveform
위의 Waveform은 일반 Sine Waveform보다 평균(Average, = 0)에 밀집해 있습니다.
Probabilty Density Curve를 보면 음수(Negative) 방향으로 꼬리가 긴 형태의 분포해
비대칭을 이루고 있다는 것을 알 수 있습니다.
이러한 분포로 인해 해당 Waveform의 Skewness는 음수로 -1.134가 됩니다.
Kurtosis, 첨도
0. 기본 개념
Kurtosis, 첨도란?
Sampling 된 Waveform 데이터의 분포가 평균(Average)에 몰려있는 정도를 나타내는 척도입니다.
그래프에서 뾰족한 정도를 의미합니다.
(출처: rfriend Tistory)
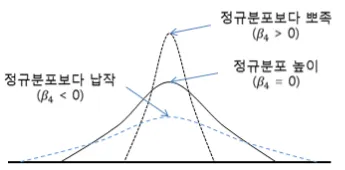
첨도는 일반적으로 통계량이 명확하게 나타나지 않기 때문에 해석에 논란의 여지가 있습니다.
그래서 독단적인 지표로 사용하기 보다는 보조적인 의미로 해석해야 합니다.
정규분포의 높이는 3이지만 일반적으로 계산에 용이하도록 0으로 맞추기 때문에 -3을 적용합니다.
그래서 정규분포의 높이를 0, 즉 정규분포의 첨도가 0(Zero)이라고 했을 때,
•
첨도가 0보다 큰 경우, 정규분포보다 뾰족한 경우로 데이터가 평균에 밀집된 상태입니다.
•
첨도가 0보다 작은 경우, 정규분포보다 납작한 경우로 데이터가 평균에 밀집되지 않고 퍼져 있는 경우입니다.
진동 분석에서의 Kurtosis 사용 용도
값에 따라 진동 Waveform에서 이상 값이 발생할 가능성에 대한 지표로 해석할 수 있으며
특히, Waveform 내의 충격성 진동을 확인할 수 있는 지표입니다.실제 분석에 적용을 해보면 다음과 같습니다.
1. Sine Waveform
위에서 설명해 드렸던 Sine Waveform입니다.
균등분포(Uniform)의 경우 첨도는 -9/5로 -1.8의 값을 가집니다.
위와 같은 Sine Waveform은 정규분포보다는 균등분포에 가까운 분포를 가지고 있기 때문에
Sine Waveform의 Kurtosis는 -1.5의 값을 가집니다.
2. MotorSense Example Waveform
해당 Waveform의 경우 진폭이 평균(Average)인 0에 대부분 밀집되어 있으며 갑자기 튀는 진동이 나타난 것을 볼 수 있습니다.
이러한 충격성 진동으로 인해 해당 Waveform의 Kurtosis는 정규분포의 첨도 값보다 큰 값(218.918)을 가집니다.
Crest Factor, 파고율
0. 기본 개념
Crest Factor, 파고율이란?
Waveform의 RMS에 대한 Peak 진폭의 비율을 의미하며,
Peak-to-RMS ratio라고도 합니다.
파고율은 진동의 평균 수준(RMS) 대비 순간 최고 수준(Peak)을 비교함으로써 Waveform에서 발생하는 상대적인 충격의 양을 파악할 수 있습니다.
즉, 최고 수준(Peak)이 평균파형에 비해 얼마나 극단적인지를 나타냅니다.
진동 분석에서의 Crest Factor 사용 용도
진동 Waveform에서 Kurtosis와 마찬가지로 충격성 진동을 확인할 수 있는 지표입니다.
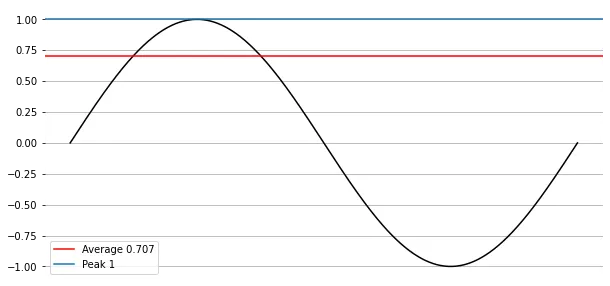
충격성 진동은 Crest Factor만을 사용해서 찾아낼 수 없기 때문에 Kurtosis 등 다양한 지표를 적용하여 판단합니다.1. Sine Waveform
진폭이 1인 Sine Waveform의 경우, RMS는 0.707이며, Peak 는 1이므로
Crest Factor는 로 1.414입니다.
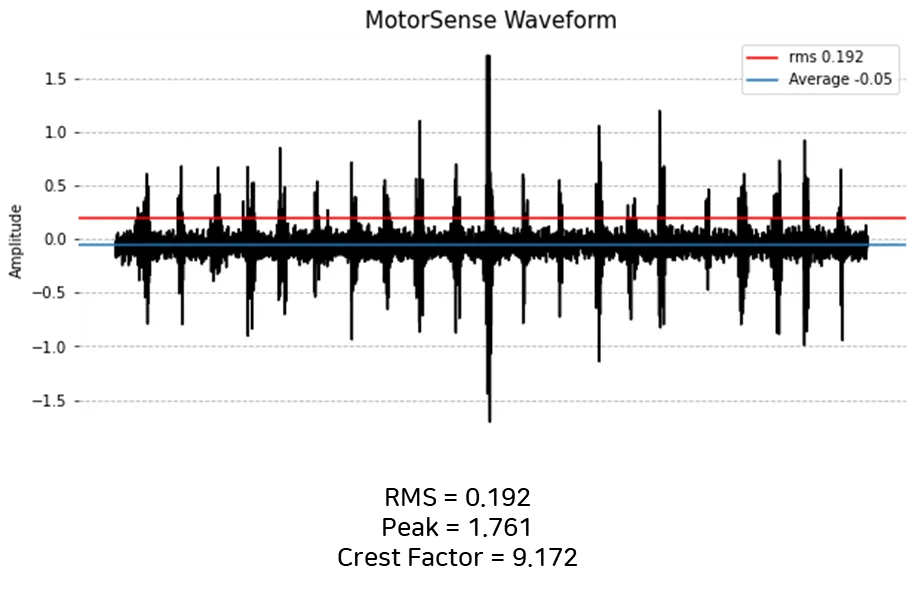
2. MotorSense Example Waveform
위의 그래프의 경우,
1초동안 튀는 진동이 많은 진동 Waveform이기 때문에 일반 Sine Waveform보다는 큰 Crest Factor를 가지는 것을 알 수 있습니다.
RMS 대비 Peak, 즉 Crest Factor는 9.172의 값을 가집니다.
정리
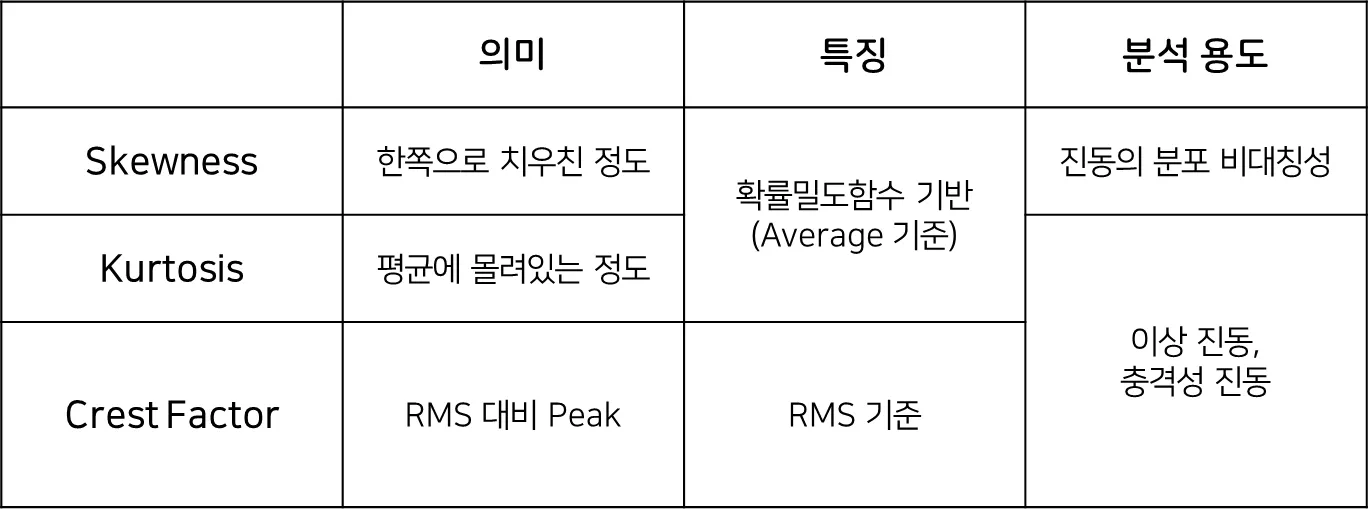
Skewness나 Kurtosis 같은 경우 Average 평균을 기준으로 값을 도출하지만
Crest Factor의 경우 RMS를 기준으로 값을 도출합니다.
그래서 Skewness와 Kurtosis의 크기가 꼭 Crest Factor 값과 비례하지 않을 수도 있습니다.
예시 Waveform의 정리
지금까지 진동 크기 외의 분석 지표에 대해 알아봤습니다.
모터센스에 대해 더 자세히 알고 싶으시다면 아래 버튼을 클릭해 홈페이지에 방문해주세요
