안녕하세요, AI 기반 예지보전 솔루션 모터센스입니다.
지난번에는 진동의 요소와 발생 원인에 대해 알아봤습니다.
만약 해당 게시글을 보지 않았다면, 아래의 링크를 참고해 주세요.
오늘은 진동의 기본인 단진동과 정현파에 대해 알아보고자 합니다.
단진동과 정현파에 대해 알아보기 전에
등속 원운동의 정의를 먼저 하겠습니다.
등속 원운동
등속 원운동
어떤 물체가 한 점을 중심으로 일정한 속력을 갖고 회전하는 원운동
일상생활에서 볼 수 있는 예시로는
관람차, 세탁기 속 빨랫감, 자이언트 스윙 등이 있습니다.
관람차, 세탁기 속 빨래감 (출처: Freepik)
단조화진동 (단진동)
그렇다면 단조화진동(단진동)은 무엇일까요?
단조화진동 (단진동)
등속 원운동을 하는 물체를 옆에서 보면 일직선상에서 위, 아래로 왕복하는 운동으로 보이는 진동
출처: 숭실대학교 물리학 강의 자료
좀 더 쉽게 설명하자면,
(가)
등속 원운동을 하는 물체가 있을 때, 눈으로 움직이는 방향은 원 모양 입니다.
(나)
이것을 각도를 틀어서 옆에서 볼 때는
물체가 위아래로만 움직이는 것처럼 보입니다.
이렇게 옆에서 볼 때 등속 원운동이 위아래로만 움직일 때의 모습을 "단진동" 이라고 합니다.
(다)
이 단진동에서의 위, 아래의 위치를 변위라고 하는데요.
이렇게 위아래로만 움직이는 단진동을 변위와 시간의 흐름으로 그래프로 나타낸 것이 정현파 입니다.
정현파 (Sinusoidal Signal)
정현파(Sinusoidal Signal)를 다시 정의하자면,
등속 원운동(원형 회전)을 할 때, 원의 x축 또는 원의 y축의 변화를 시간에 따라 파형을 그래프로 표현한 것입니다.
흔히 삼각함수의 Sine 그래프와 Cosine 그래프가 이에 해당합니다.
출처: 공돌이의 수학 정리노트
위 영상에서 보면, 등속 원운동으로 얻을 수 있는 파형은 2개입니다.
•
x축을 기준으로 시간에 따른 변화는 Cosine 그래프 파형
•
y축을 기준으로 시간에 따른 변화는 Sine 그래프 파형
Sine 그래프, Cosine 그래프 (출처: MotorSense)
정현파 (Sinusoidal Signal)의 3가지 요소
이렇게 얻어진 정현파의 구성 요소는 A (진폭)와, ω (주파수), ∅ (위상) 3가지입니다.
진폭 (Amplitude), A
진폭(Amplitude)은 진동의 크기를 의미합니다.
정현파의 진폭은 회전하는 원의 반지름의 길이와 같습니다.
주파수 (Frequency), ω
주파수(Frequency)는 1초에 완성되는 주기(T)의 개수를 의미합니다.
여기서 주기(T)는 한 번의 cycle을 완성하는 데 필요한 시간을 말합니다.
즉, 주파수는 회전 속도와 관련이 있으며,
회전 속도가 빠를수록 주파수가 커집니다.
주파수는 주기의 역수이며, 단위는 Hz(헤르츠)를 사용합니다.
출처: 공돌이의 수학정리
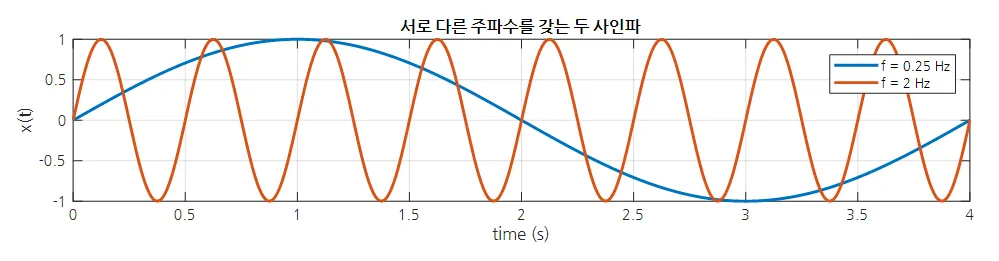
위의 그래프를 보면, 4초에 1회의 주기를 가지며, 1Hz는 1초에 0.5회의 주기를 가집니다.
위상 (Phase), ∅
위상(Phase)은 등속 원운동을 할 때의 시작점을 의미합니다.
다시 말해,
등속 원운동을 하는 물체가 어디서부터 출발을 한 것인가를 보여주는 요소입니다.
단위는 °(degree, 도)를 사용합니다.
서로 다른 위상을 갖는 원의 회전에 대한 Sine 그래프 (출처: 공돌이의 수학 정리노트)
같은 Sine 그래프이지만 그래프가 다르게 보이는 이유는
회전 시작 위치가 다름, 즉 위상 (∅)이 다르기 때문입니다.
변위, 속도, 가속도의 관계
수학적인 진동 모델 식에서는 질량 요소(m)의 변위에 대한 정현파 식으로 진동 현상을 정의합니다.
하지만, 진동 측정에 사용되는 진동 센서의 종류에 따라 물리량이 달라집니다.
따라서 분석 목적에 맞는 진동 센서로 데이터를 수집하는 것을 권장합니다.
부득이한 경우에는 측정된 진동 데이터를 다른 진동 물리량으로 변환하여 사용합니다.
예를 들면, 진동 가속도계로 측정된 진동 가속도를 속도로 변환하는 방식입니다.
일반적인 운동식에서 변위, 속도, 가속도의 경우
변위를 미분하면 속도, 속도를 미분하면 가속도를 계산할 수 있습니다.
이 관계는 진동 현상을 설명하는 정현파 식에서도 동일합니다.
이 때, 단순한 정현파 식에서 A(Amplitude)라고 표시되었던 진폭이 변환된 물리량에 따라 달라짐을 확인 할 수 있습니다.
[변위 기준식] 변위, 속도, 가속도의 관계와 공식 (출처: MotorSense)
변위 기준식에서
속도의 진폭은 주파수(ω)의 1차식인 Aω,
가속도의 진폭은 주파수의 2차식인 Aω2이 나오게 되는데
이는 측정된 진동 변위를 미분 변환할수록 진동의 주파수에 비례하여 더 큰 진폭이 나옵니다.
[변위 기준식] 가속도, 속도, 변위의 관계와 공식 (출처: MotorSense)
가속도 기준식에서
속도의 진폭은 A/ω, 변위는 A/ω2 가 나오게 되는데
이는 측정된 진동 가속도를 적분 변환할 수록 주파수에 반비례하여 더 큰 진폭이 나옵니다.
기준식을 정리하자면, 아래와 같습니다.
분석 대상에 따른 진동 물리량 (출처: MotorSense)
주파수 성분이 높은 고주파 진동일수록
사용되는 진동 물리량은 변위보다는 가속도나 속도를 사용하는 것이 분석에 유리합니다.
반대로 주파수 성분이 낮은 저주파 진동일수록
사용되는 진동 물리량은 가속도보다는 변위나 속도를 사용하는 것이 분석에 유리힙니다.
지금까지 단진동과 정현파에 대해 알아봤습니다.
모터센스에 대해 더 자세히 알고 싶으시다면 아래 버튼을 클릭해 홈페이지에 방문해주세요
