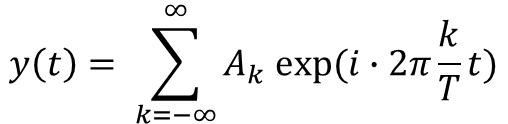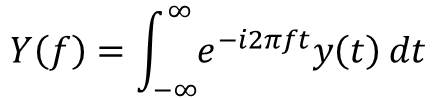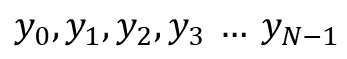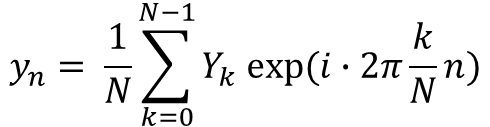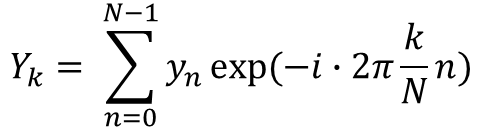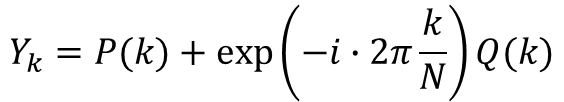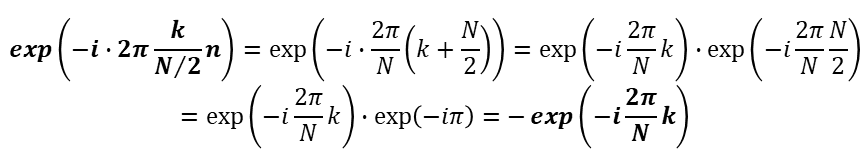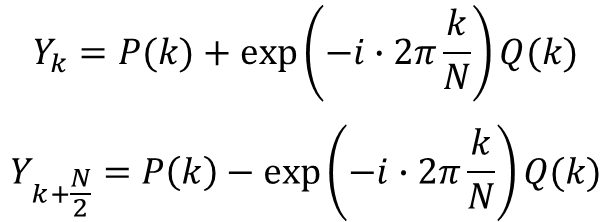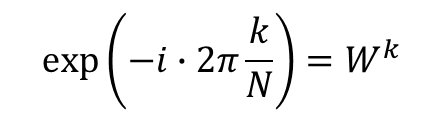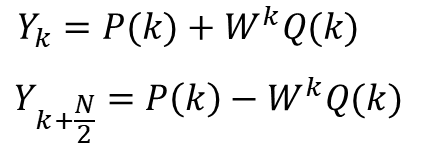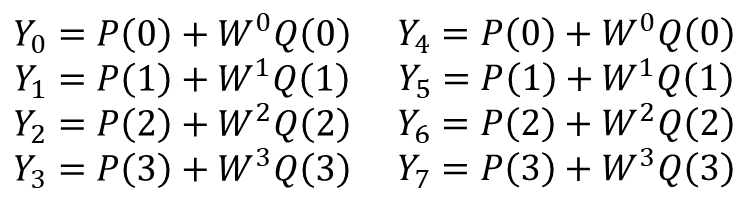안녕하세요, AI 기반 예지보전 솔루션 모터센스입니다.
지난번에는 진동 크기의 표현 방법에 대해 알아봤습니다.
만약 해당 게시글을 보지 않았다면, 아래의 링크를 참고해 주세요.
오늘은 푸리에 변환 (Fourier Transform) 에 대해 알아보고자 합니다.
이전 포스팅에서 살펴 보았듯이, 진동은 Time Domain과 Frequency Domain으로 표현할 수 있습니다.
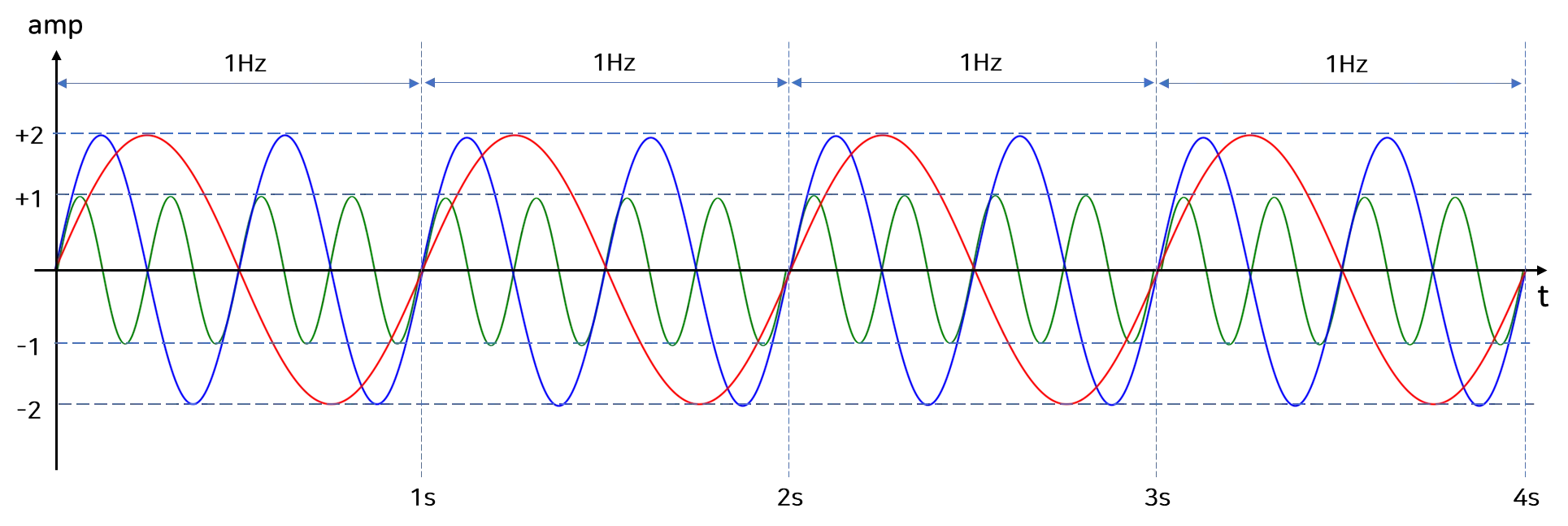
위의 이미지는 Time Domain으로 표현한 진동 Waveform입니다.
빨간색 Waveform은 1초에 1회의 주기를 가지며,
파란색 Waveform은 1초에 2회의 주기,
초록색 Waveform은 1초에 4회의 주기인 것을 확인 할 수 있습니다.
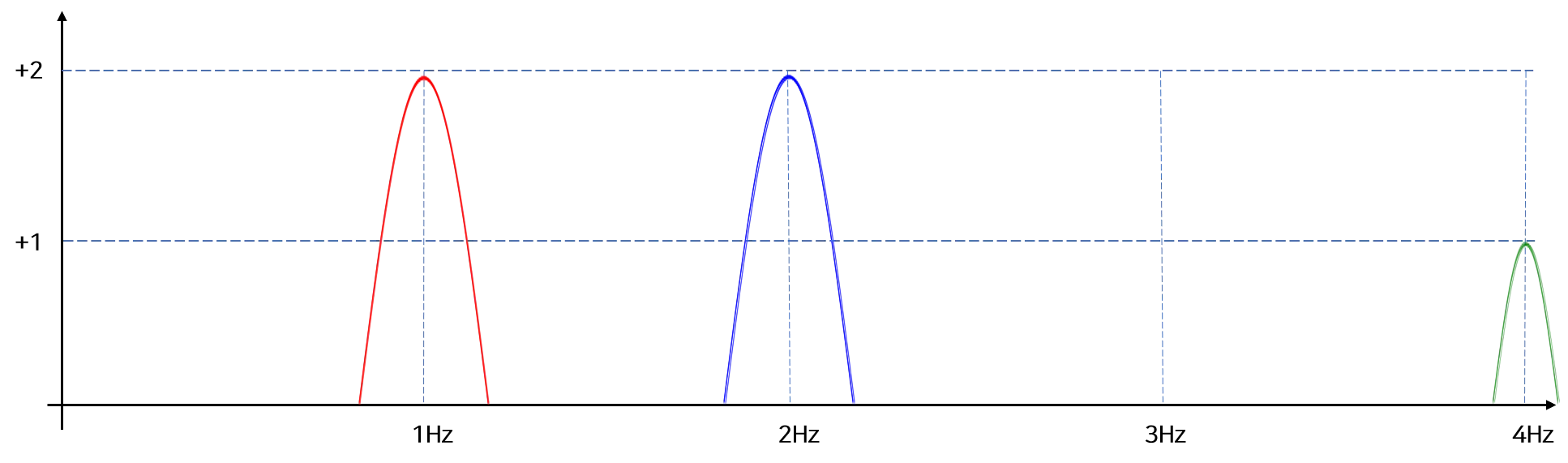
해당 Waveform을 변환 식을 통해 변환하여 Frequency Domain으로 표현한다면
아래와 같이 표현할 수 있습니다.
오늘은 이 변환 과정에 필요한
푸리에 변환(Fourier Transform)에 대해 알아보도록 할까요?
 Fourier Transform
Fourier Transform
 푸리에 변환(Fourier Transform)이란?
푸리에 변환(Fourier Transform)이란?
Time Domain으로 표현된 Waveform을 Frequency Domain으로 변환하는 방법
주기 T를 가지고 반복되는 모든 신호 ()는
아래와 같이 주파수와 진폭이 다른 여러 개의 신호의 합으로 나타낼 수 있습니다.
시간에 따른 연속적인 신호(Time Domain)을 Frequency Domain으로 변환하는 방법은 아래와 같이 정의됩니다.
이러한 푸리에 변환 방식은 수식에서도 볼 수 있듯이 ‘연속 시간에 대한 신호’를 위한 변환 방식입니다.
하지만 디지털 장치(컴퓨터, 계측기 등)는 연속적인 신호를 측정 및 처리할 수 없으며 이산 신호에 대해서만 가능합니다.
그래서 위와 같은 무한 신호에 대한 푸리에 변환식이 아니라 이산 신호를 처리할 수 있는 이산 푸리에 변환(Discrete Fourier Transform)을 통해 변환을 해야 합니다.
여기서 잠깐! 이산 신호란 무엇일까요?
•
이산 신호: 시간과 시간 사이가 연속이 아닌, 간격이 있는 신호를 의미
◦
일반적으로 음악, 영상 등도 이에 포함됨
◦
유한한 간격을 가진 시간 신호를 연결하여, 사람이 인지하지 못할 정도로 짧게 붙여 연속적인 신호인 것처럼 보이게 한 것
◦
컴퓨터에서 다루어지는 모든 신호 = 이산 신호
1. 이산 푸리에 변환 (Discrete Fourier Transform, DFT)
이산 푸리에 변환은 시간이 N인 이산 시간 데이터가 있을 때,
위와 같이 수많은 신호들이 주기 N으로 반복된다는 가정하에 푸리에 변환을 하는 것입니다.
하나의 이산 신호는 주파수와 진폭이 서로 다른 N개의 사인 함수들의 합으로 나타낼 수 있습니다.
그리고 이 식에서 진폭 를 원래 데이터에 대한 푸리에 변환값이라고 합니다.
이산 푸리에 변환의 경우, 연산량이 많기 때문에 속도가 매우 느리다는 단점이 있습니다.
이 과정을 더 빠르게 해결하기 위해 고안된 방법이 고속 푸리에 변환(FFT)입니다.
2. 고속 푸리에 변환 (Fast Fourier Transform, FFT)
 고속 푸리에 변환 (Fast Fourier Transform, FFT)이란?
고속 푸리에 변환 (Fast Fourier Transform, FFT)이란?
Sampling 된 신호 전부를 변환시키는 것이 아니라,
필요한 신호를 골라 고속으로 푸리에 변환 연산을 하는 방법입니다.
최근에는 방대한 데이터를 처리하는 경우가 많기 때문에
속도가 빠른 고속 푸리에 변환을 훨씬 자주 사용합니다.
고속 푸리에 변환에는 수많은 방식들이 있으며,
그 중 이산 푸리에 변환에 분할 정복 알고리즘을 추가하여 속도를 높인 변환 방법을 소개하고자 합니다.
 분할 정복 (Divide and Conquer) 알고리즘
분할 정복 (Divide and Conquer) 알고리즘
 분할 정복 (Divide and Conquer) 알고리즘이란?
분할 정복 (Divide and Conquer) 알고리즘이란?
이 방법은 1965년 J.W.Cooly와 J.W.Tukey가 발표하여 널리 알려진 것으로
데이터의 크기 n을 재귀적으로 2등분 하여 적은 계산량으로도 비슷한 값을 도출할 수 있는 알고리즘입니다.
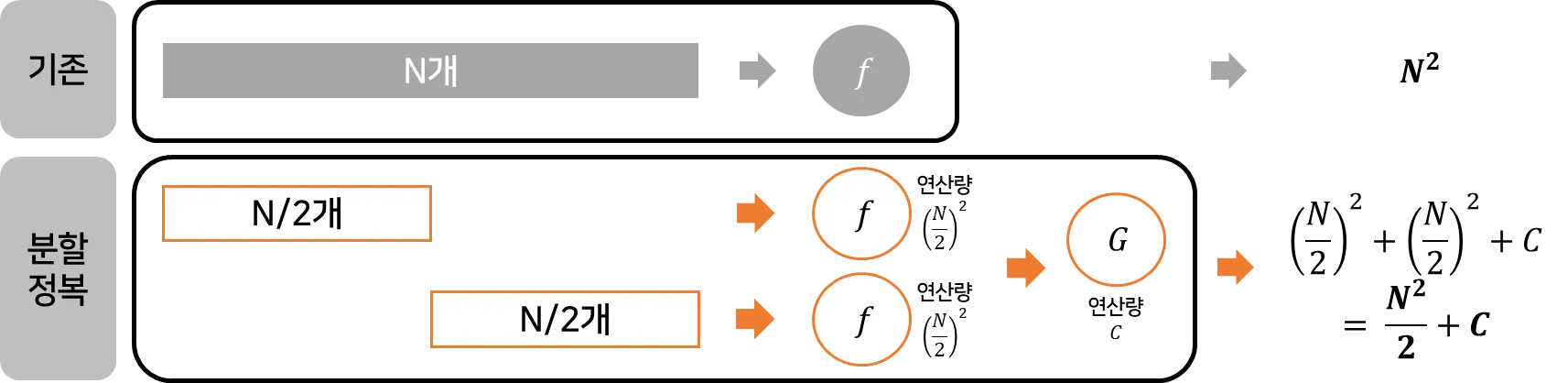
해당 알고리즘에 대해서 표현하자면,
N개의 데이터일 때의 계산량은 이지만,
분할 정복 알고리즘을 이용하면 로 줄어들게 되는 것을 확인할 수 있습니다.
고속 푸리에 변환은 재귀적으로 2등분을 하는 분할 정복 알고리즘을 기반으로 하므로
길이가 인 신호에 더 쉽게 적용할 수 있습니다.
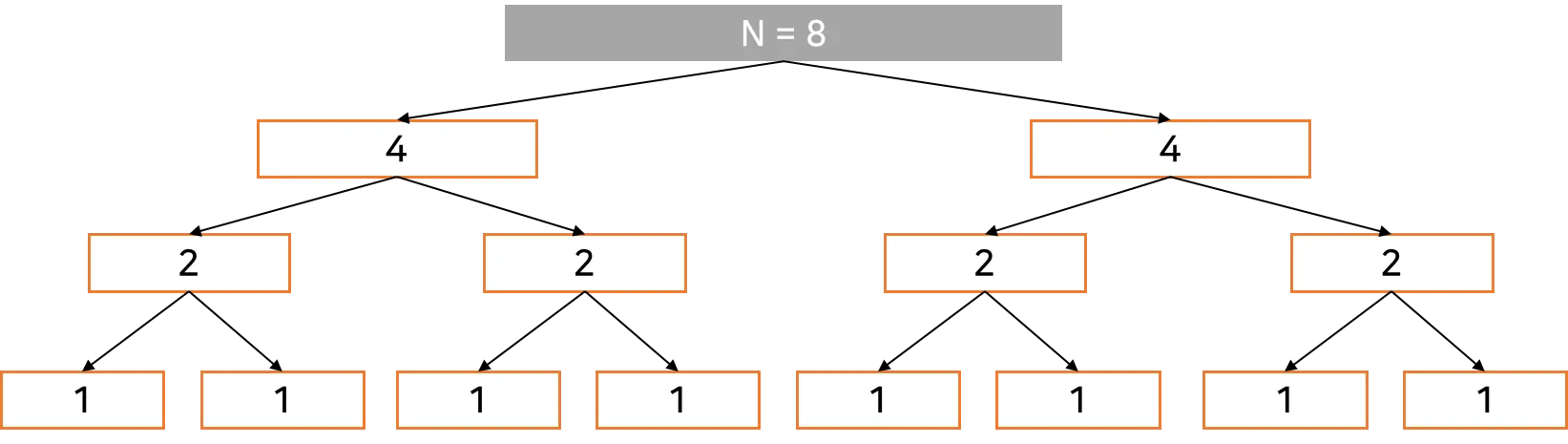
예를 들어 길이가 8인 데이터를 분할 정복 알고리즘을 이용할 때,
위의 이미지에 나타난 과정으로 분할 및 계산한다는 의미입니다.
즉, 2등분을 하는 작업()을 개의 개수만큼 반복되기 때문에 만큼 계산됩니다.
이 분할 정복 알고리즘을 이산 푸리에 변환에 적용함으로써 고속 푸리에 변환 식이 만들어지게 되었습니다.
해당 유도식을 간략하게 보자면, 아래와 같습니다.
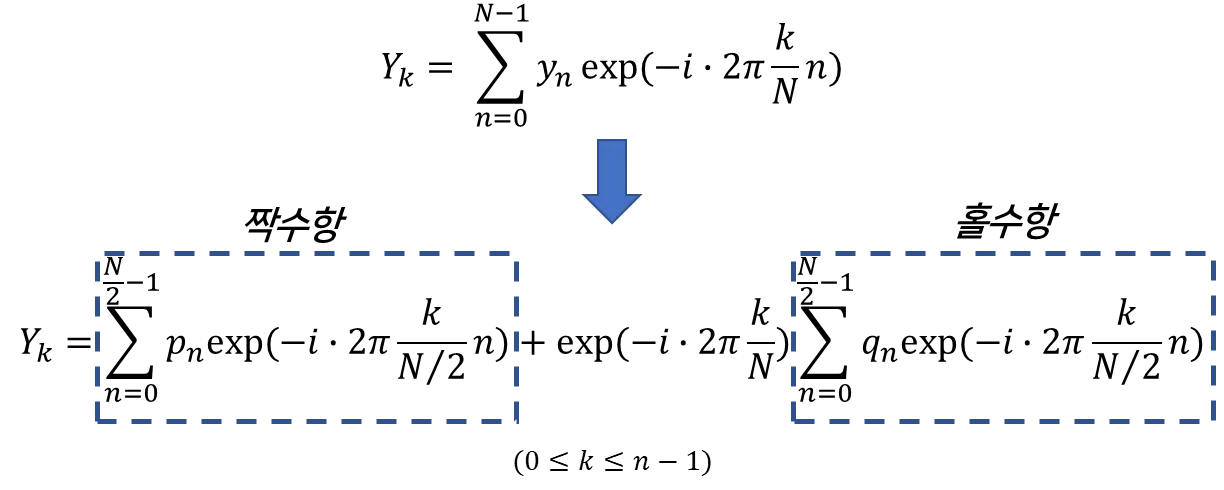
신호의 샘플링된 데이터가 과 같이 있을 때,
이산 푸리에 변환값을 위의 짝수, 홀수 식으로 구분해서 작성하면 아래와 같습니다.
자세히 해당 식을 보면 개의 짝수 항에 대한 이산 푸리에 변환 값과
개의 홀수 항에 대한 이산 푸리에 변환 값에 상수()를 곱한 식으로 이루어져 있습니다.
짝수 항에 대한 변환 값을 , 홀수 항에 대한 변환값을 라고 하면 아래와 같이 정리할 수 있습니다.
개의 데이터를 의 길이를 가진 두 개의 이산 푸리에 변환 식의 합으로 표현한 것입니다.
이산 푸리에 변환에서는 주기성과 복소지수함수의 성질이 내포되어 있습니다.
•
주기성 성질
개의 원소에 대한 이산 푸리에 변환 : 의 주기를 가집니다.
•
복소지수함수 성질
이 두 가지 성질을 이용하여, 위의 식을 다시 표현하여,
이 식에서 지수함수 부분을 로 대치하면 아래와 같습니다.
예를 들어 N이 8인 신호를 계산한다면, 아래와 같이 계산이 가능합니다.
N이 8개일 때, 4개의 P, W, Q를 가지고 계산을 할 수 있습니다.
이러한 일련의 과정을 반복하여
이산 푸리에 변환의 계산량인 를
고속 푸리에 변환을 이용하여 로 줄일 수 있게 됩니다.
지금까지 푸리에 변환 (Fourier Transform) 에 대해 알아봤는데요.
신호를 변환하는 과정은 이렇게 복잡하지만, 이 과정을 거쳐 고장을 분석하는 예지보전 솔루션 ‘모터센스’는 누구나 사용할 수 있을 만큼 몹시 간단하답니다 :)
모터센스에 대해 더 자세히 알고 싶으시다면 아래 버튼을 클릭해 보세요