지난번에는 푸리에 변환 (Fourier Transform)에 대해 알아봤습니다.
만약 해당 게시글을 보지 않았다면, 아래의 링크를 참고해 주세요.
오늘은 Spectral Leakage와 Window Function에 대해 알아보고자 합니다.
디지털 장치는 연속적인 신호에 대해서 계측 또는 연산을 할 수 없어,
기존의 연속 시간에 대한 신호를 위한 푸리에 변환(Fourier Transform) 대신 이산 푸리에 변환(Discrete Fourier Transform)을 사용한다는 내용이었습니다. 
해당 내용에 대해서 좀 더 자세히 설명해 보겠습니다.
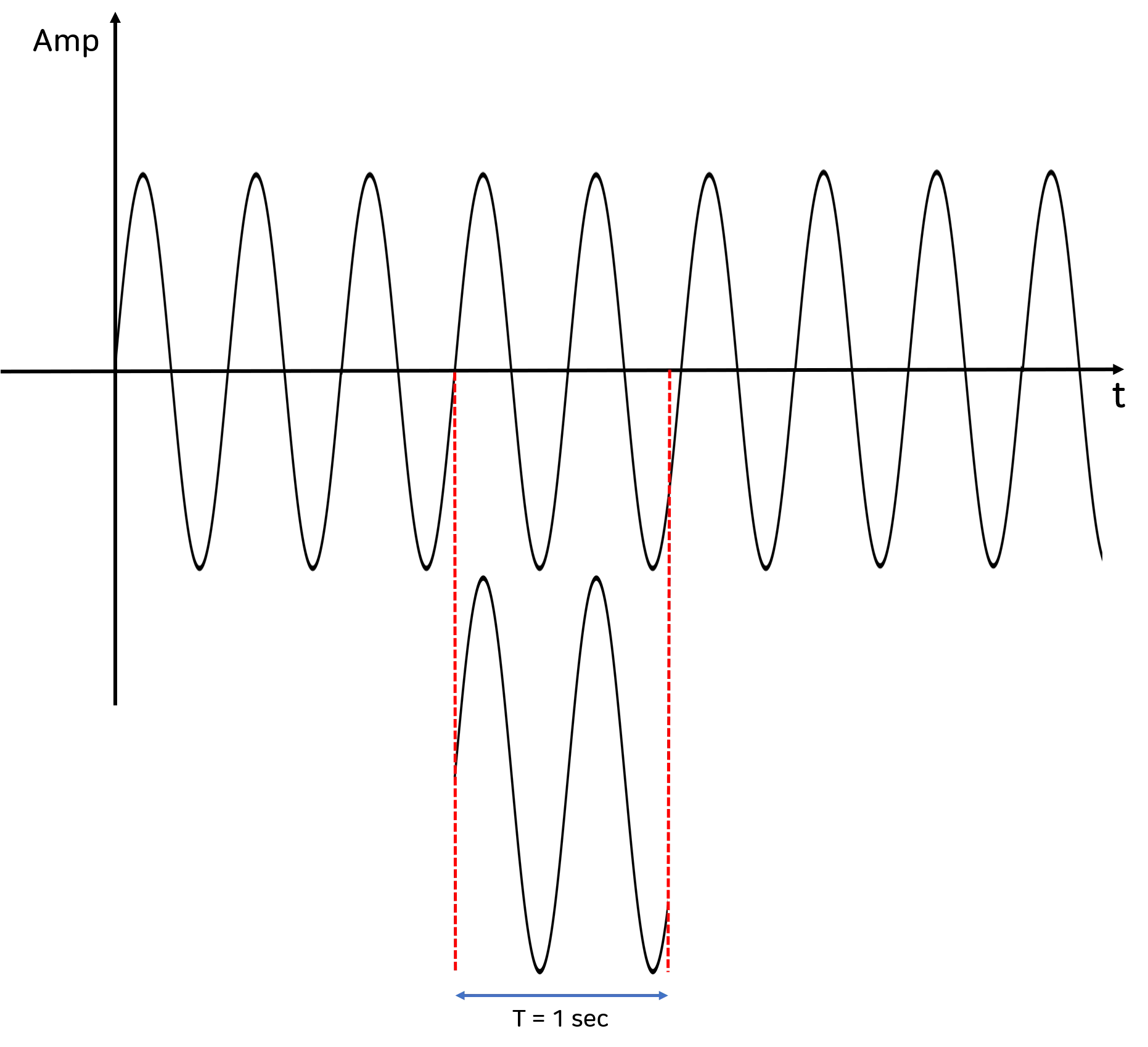
위 이미지의 상단 그래프와 같이 실제 진동 데이터는 연속적으로 나타나는 ‘무한 신호’입니다.
하지만, 우리가 디지털 장치(계측기 등)으로 얻을 수 있는 데이터는
전체 데이터 중 측정을 시도한 시간 동안만 수집된 ‘유한 신호’입니다.
전체 데이터 중 극히 일부인 것이죠.
(MotorSense의 경우 1초를 측정합니다.)
하지만, 신호가 무한히 이어진다고 측정도 무한하게 하는 것은 현실적으로 무리가 있습니다.
그래서 데이터를 측정하지 못한 측정 전,후 시간 동안 발생한 신호에 대해서는 ‘추정’을 통해 유추할 수 있습니다.
푸리에 변환(Fourier Transform)은 신호가 주기성을 갖고 반복된다는 가정을 바탕으로
측정한 신호(유한 신호) 가 측정하지 못한 시간 동안에도 반복된다고 추측해 나머지 신호를 알아내는 방식입니다.
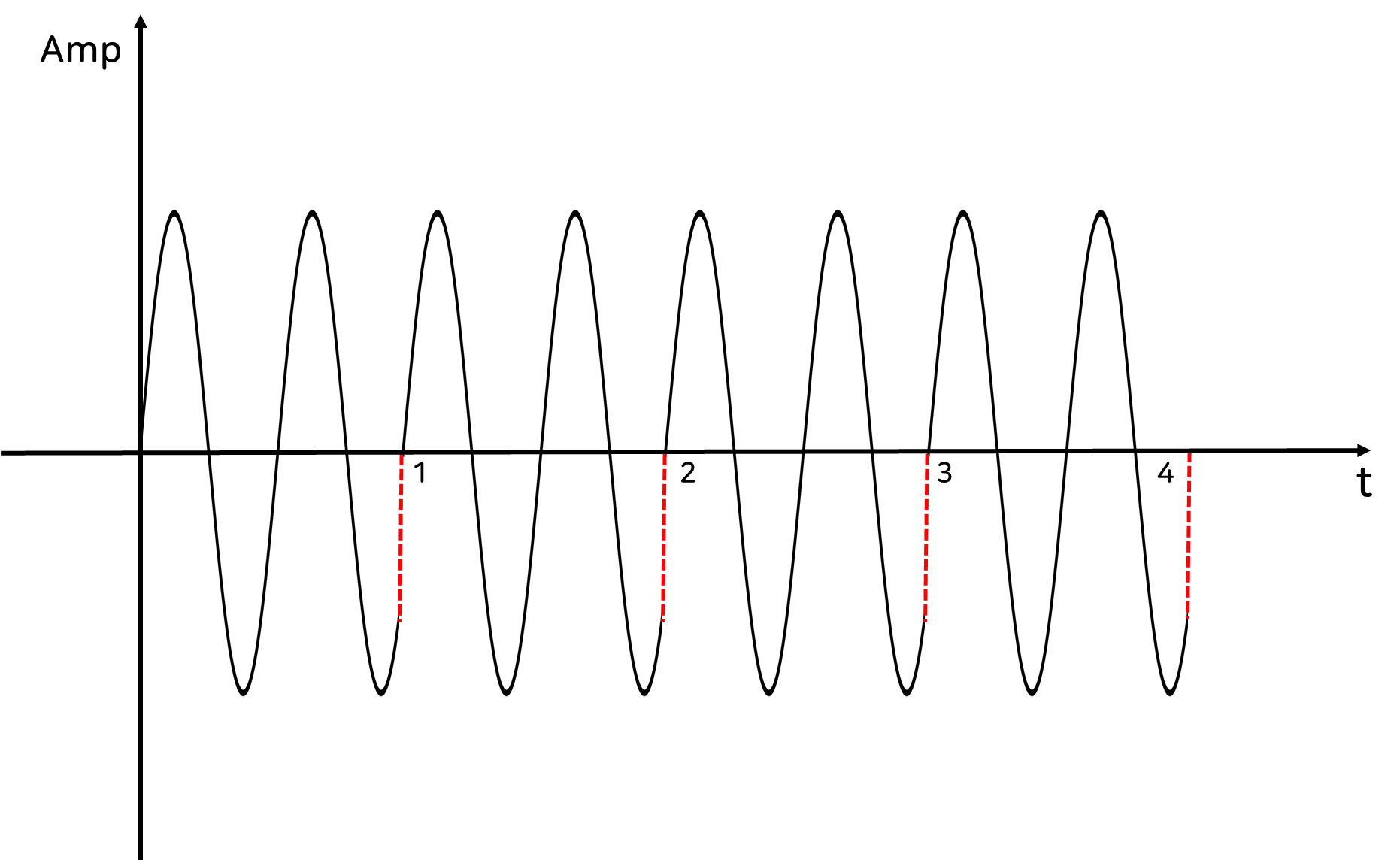
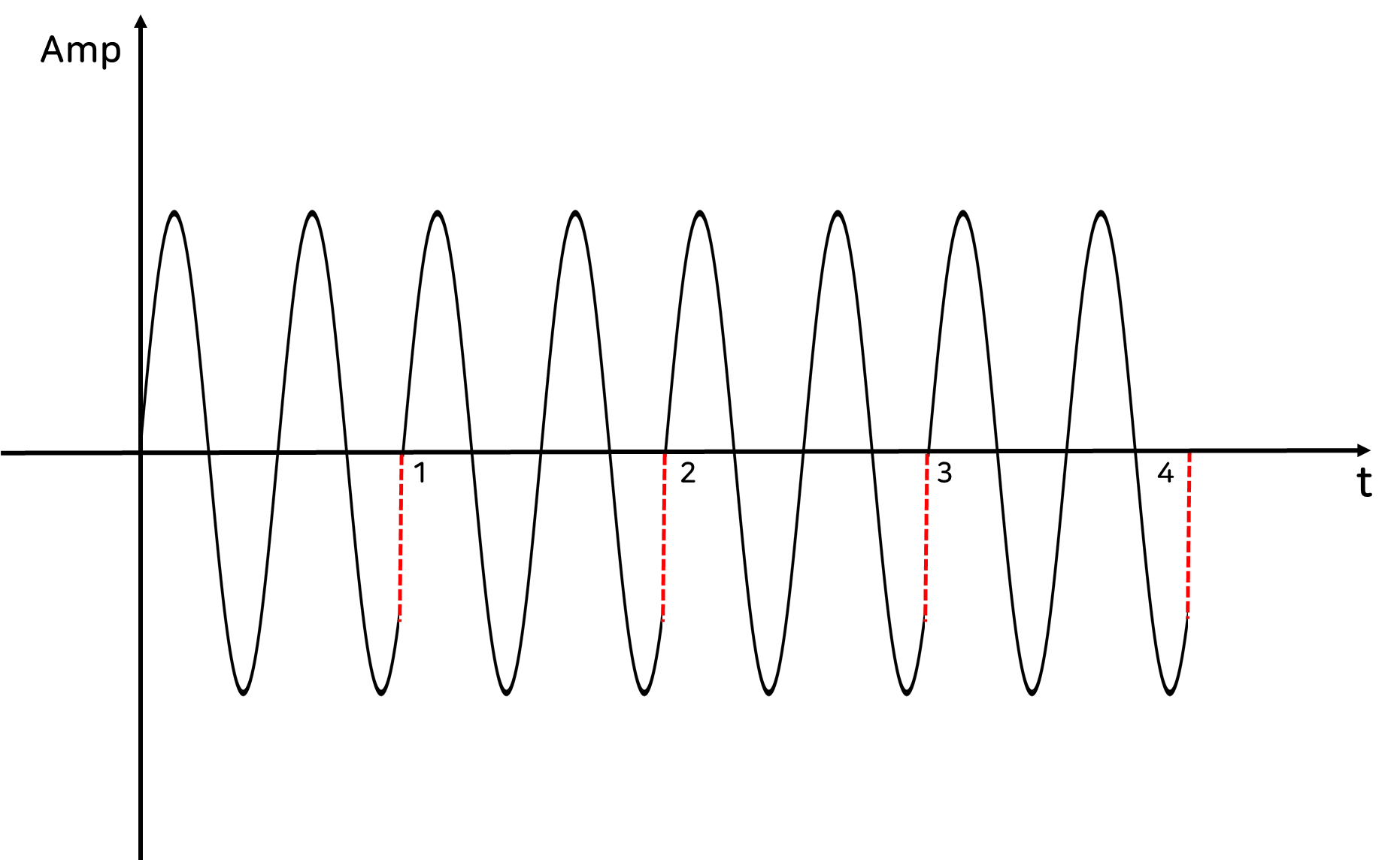
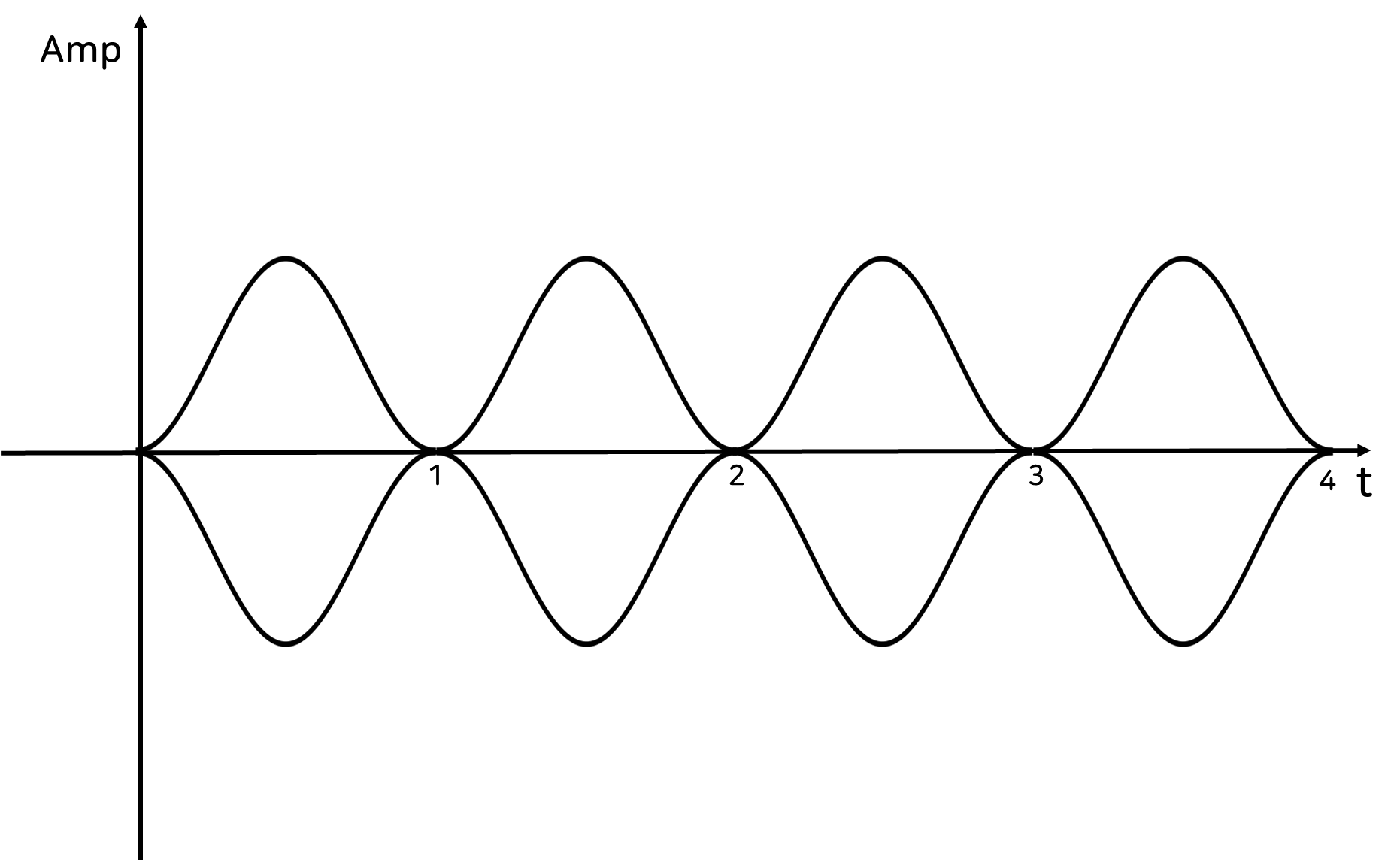
즉 측정한 신호를 아래의 이미지와 같이 이어 붙여서 무한 신호로 만들어냅니다.
이렇게 유한 신호를 무한 신호의 형태로 바꾼 후, 푸리에 변환을 통해 Frequency Domain으로 바꿀 때 Spectral Leakage 현상이 나타나게 되는데요.
Spectral Leakage란 무엇이고, 이 현상은 어떻게 해결하면 될까요?
 Spectral Leakage란?
Spectral Leakage란?
Time Domain → Frequency Domain 변환시,
원래의 신호에는 포함되어 있지 않은 주파수 성분이 관측되는 현상을 의미합니다.
이는 원래의 주파수 성분의 에너지가 완전히 관측되지 않는 문제를 가지고 있습니다.
원인 1. 측정 시간
예를 들어,
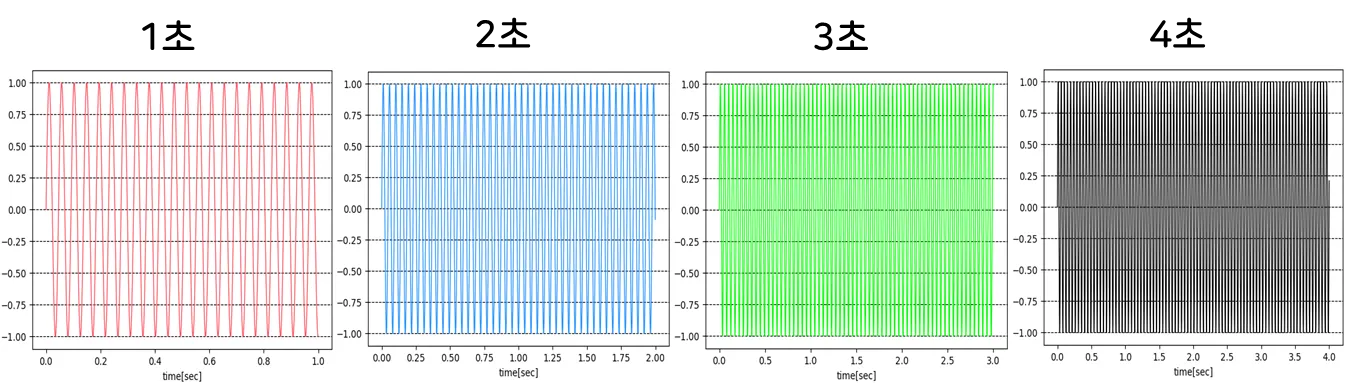
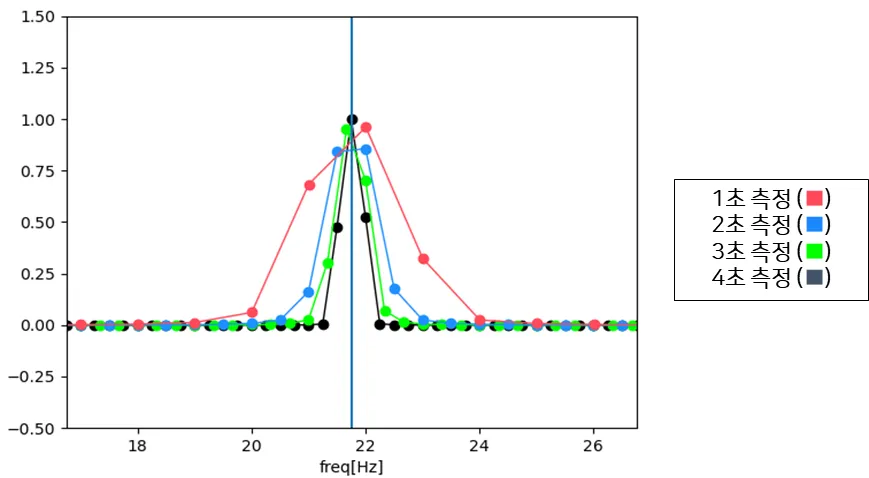
Sampling Rate가 3330일 때 약 22Hz의 Waveform을 만들고,
이를 Fast Fourier Transform(고속 푸리에 변환)을 하면
아래와 같은 Frequency Domain을 얻을 수 있습니다.
자세히 보면,
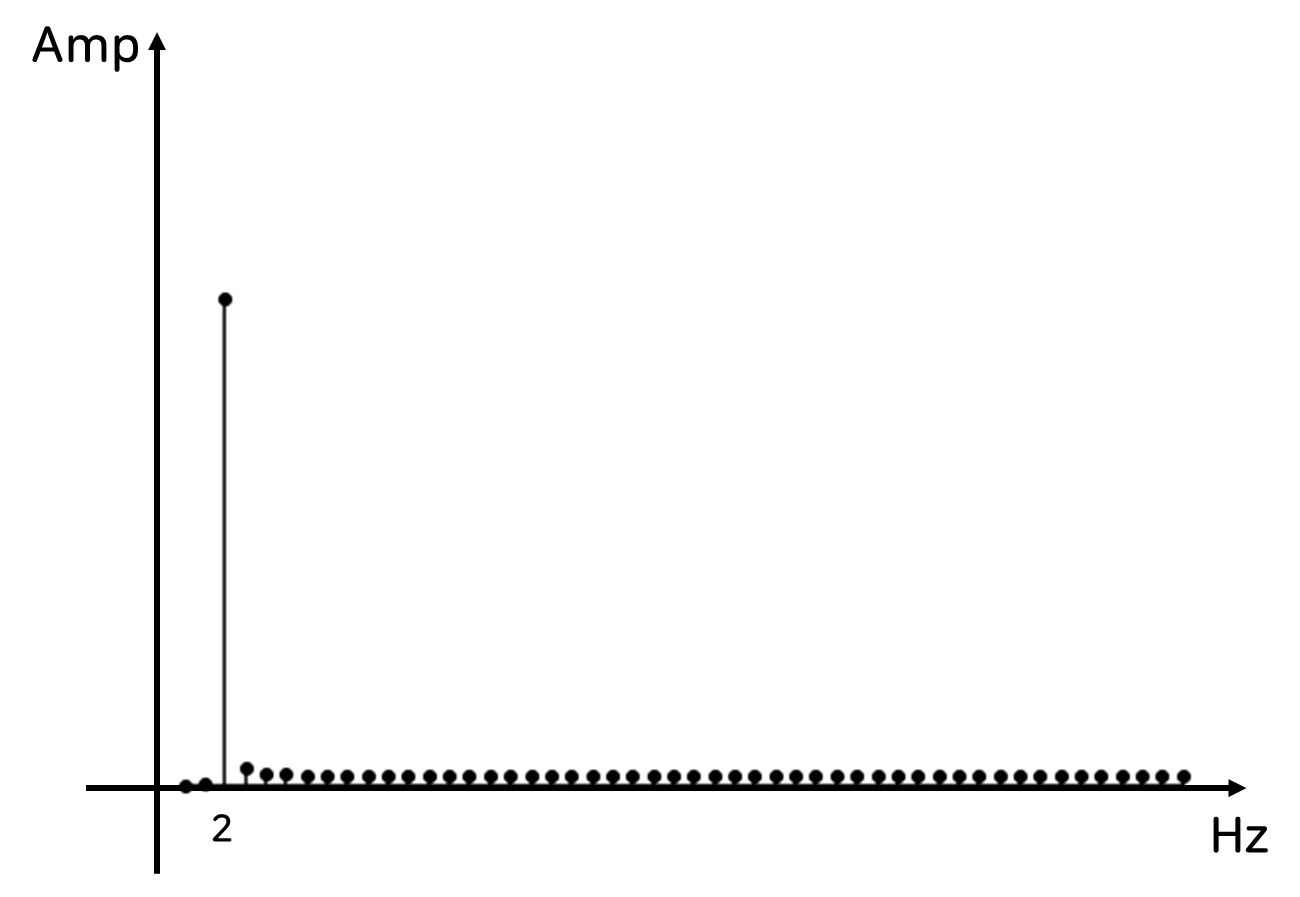
1초 측정된 Frequecy Domain은 19Hz부터 24Hz까지 퍼짐현상이 있지만,
4초 측정된 Frequency Domain은 거의 정확하게 Peak 값 (= Amplitude 1)이 나타납니다.
위에서 볼 수 있듯이,
이러한 Leakage 현상은 Fourier Transform 으로 인한 문제보다는
측정 시간이 제한적이기 때문입니다.
Time Domain을 Fourier 수식을 이용해 Fourier Transform할 때,
주파수의 시간 적분의 범위는 이론적으로 - 부터 + 까지 입니다.
하지만 실제 현장에서 진동을 무한대로 측정하는 것은 불가능하기 때문에 Spectral Leakage 현상이 발생합니다. 즉 계산식에서는 시간이 무한대로 적용되는데, 실제 현장에서 측정한 시간이 유한하다 보니 그 시간만큼 파형이 그려내는 범위에 누락이 발생하는 것이죠.
파도가 철썩~하고 칠 때 사진을 찍으면, 파도가 오르내리는 전체 파형이 아닌 최고점 한 순간만 찍히게 될 텐데요. 이와 같은 현상이라고 보시면 되겠습니다.
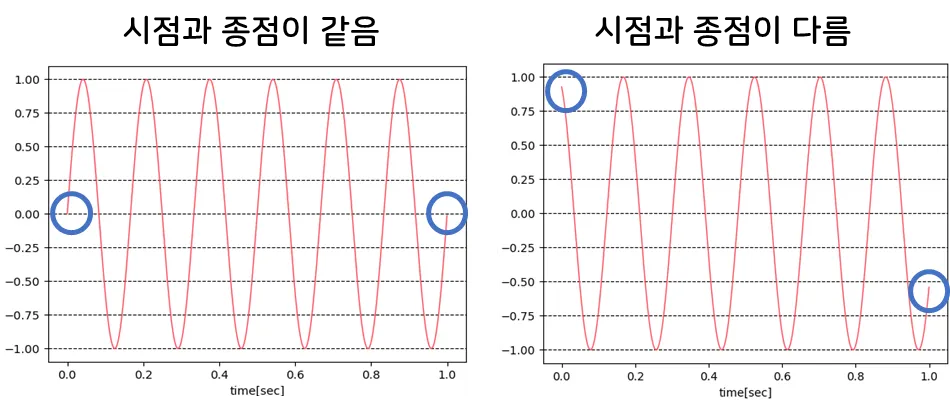
원인 2. 파형의 시점과 종점 불일치
Fourier Transform에 무한대의 시간을 근사식(유한대의 시간)으로 전환할 때 측정 그래프의 시작점과 종점이 같아야 한다는 전제가 있습니다.
하지만 실제 현장에서의 진동을 측정할 때,
이론처럼 Waveform의 시점과 종점이 딱 떨어지는 이상적인 결과를 관측하기는 어렵습니다.
특히 실험실이 아닌,
실제 공장 환경에서는 시점과 종점이 같은 이상적인 Waveform이 나타나는 경우는 거의 없습니다.
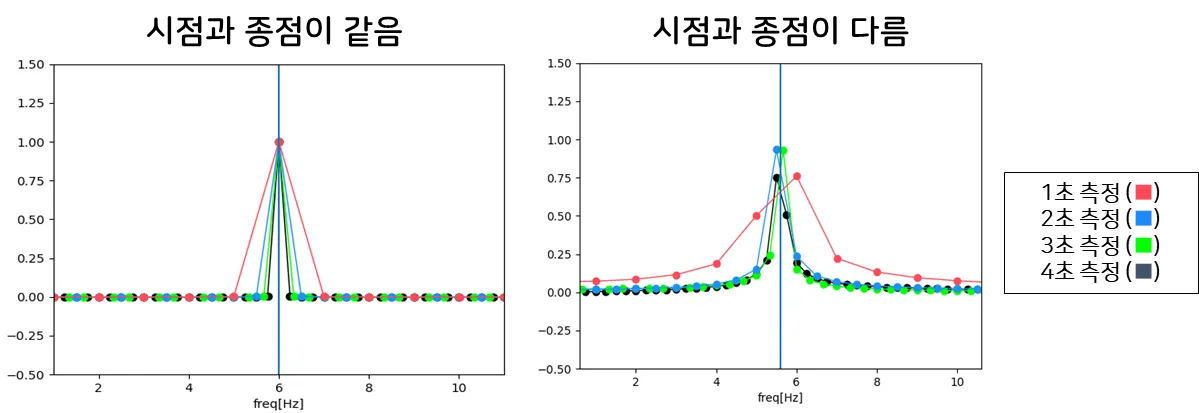
시점과 종점이 같은 경우 Leakage 현상이 거의 없지만,
시점과 종점이 다른 경우 Leakage 현상이 나타나는데요.
그래서 고속 푸리에 변환하여 얻은 Spectrum은 원래 신호의 실제 Spectrum이 아닌 ‘얼룩진 버전’이라고 할 수 있습니다.
이런 불가피한 현상을 방지하기 위한 보정 방법이 있습니다.
바로 Window Function을 사용하는 것이죠.
 Window Function
Window Function
앞서 설명했던 측정 이산 신호 그래프를 다시 보면,
1.
주기가 완전하지 않으며
2.
시점과 종점이 완벽하게 일치하지 않아 그래프의 시작점과 끝점이 동일하지 않은 것을 확인할 수 있습니다.
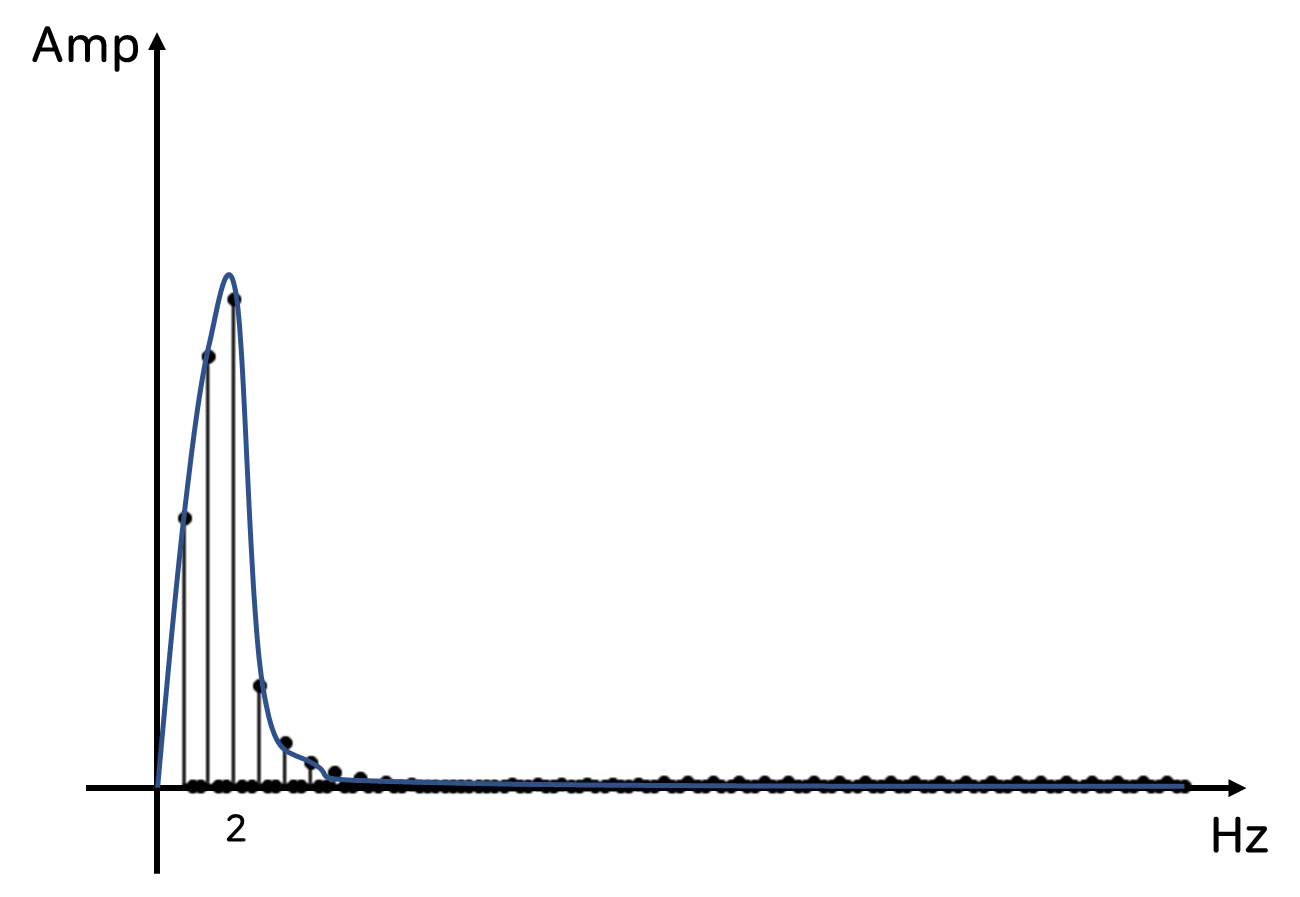
해당 신호를 그대로 고속 푸리에 변환하여 Spectrum을 추출하면, 2Hz를 중심으로의 퍼짐 현상
즉, Spectral Leakage 현상이 나타나는 것을 볼 수 있습니다.
이런 경우,
Windowing 함수를 사용하여 신호의 맨 앞과 뒤의 신호를 0에 가깝게 바꾸어 급격한 전환 없이 연속적인 파형으로 바꿀 수 있습니다.
이렇게 불완전한 신호를 연속적인 파형으로 만들어주면, 신호를 보정하지 않고 그대로 사용하는 파형보다 Spectrum으로 변환했을 때 발생하는 Leakage 현상이 현저하게 줄어들 수 있겟죠!
 Window Function이란?
Window Function이란?
Time Domain에서의 이산 신호를 고속 푸리에 변환(FFT)을 사용하여 Frequency Domain으로 변환할 시, 이산 신호의 주기의 불연속적인 진폭을 줄여 연속적인 파형으로 보이게 변환하는 함수입니다.
Window Function의 Logic은 다음과 같습니다.
•
시점과 종점이 다르거나 완전한 주기를 가지지 않는 이산 신호의 경계의 진폭을 감소시킵니다.
•
신호의 가장자리를 0 또는 0에 가깝게 감소시킵니다.
•
Window Function을 적용한 신호들을 연결하면, 가장자리가 연결되면서 연속적인 파형이 생성됩니다.
Window Function은 여러 가지 있으며,
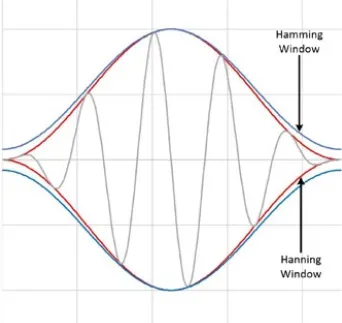
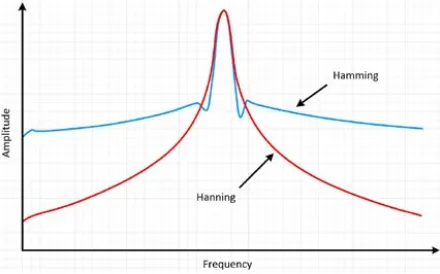
가장 많이 사용하는 Window Function은 Hanning과 Hamming 이 있습니다.
(출처: NI)
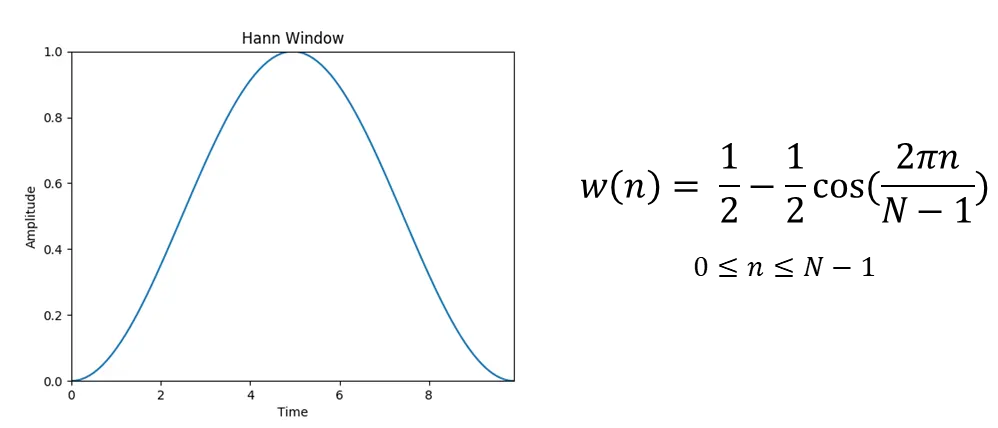
1. Hanning Window
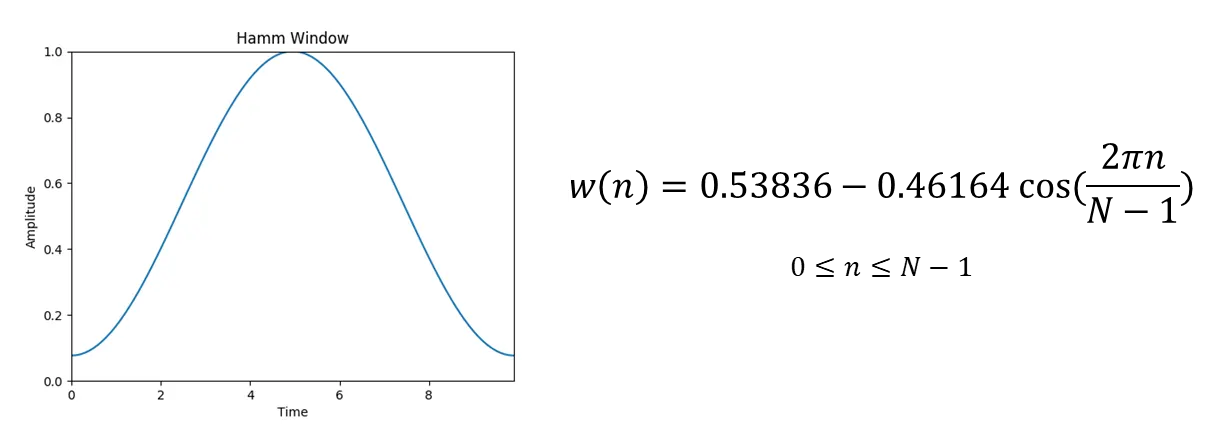
2. Hamming Window
Hamming window는 특성상 양 끝의 진폭을 0이 되지 않는 정도의 0에 가깝게 바꿔줍니다.
이러한 이유로 신호에 약간의 불연속성이 여전히 남아있습니다.
이 외의 Window Function은 여러가지 있습니다.
Window Function을 사용한다고 Leakage 현상을 완벽히 없앨 수는 없습니다.
그래서 각 Window Function의 특성을 잘 파악하여,
Data와 목적에 맞는 함수를 사용하는 것이 중요합니다.
지금까지 Spectral Leakage와 Window Function에 대해 알아봤습니다.
모터센스에 대해 더 자세히 알고 싶으시다면 아래 버튼을 클릭해 홈페이지에 방문해주세요